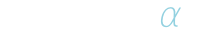utils Package¶
utils Package¶
The phantomas.utils package continas utility math functions and definitions used throughout the phantomas library.
shm Module¶
This module contains an implementation of the real, antipodally symmetric Spherical Harmonics basis as defined in [R8].
References¶
| [R8] | Descoteaux, Maxime, Elaine Angelino, Shaun Fitzgibbons, and Rachid Deriche. “Regularized, fast, and robust analytical Q-ball imaging” Magnetic Resonance in Medicine 58, no. 3 (2007): 497-510 |
- phantomas.utils.shm.L(order=4)¶
Computees the Laplace-Beltrami operator matrix.
Parameters : order : int
The truncation order (should be an even number).
- phantomas.utils.shm.P(order=4)¶
Returns the Funk-Radon operator matrix.
Parameters : order : int
The truncation order (should be an even number).
- class phantomas.utils.shm.SphericalHarmonics(coefficients)¶
This class describes a symmetrical spherical function by its spherical hamonics coefficients.
Parameters : coefficients : array-like, shape (R, )
The coefficients vector of the spherical harmonics function. The order in which the coefficients are stored is described in j().
Methods
angular_function(theta, phi) Returns the values of the spherical harmonics function at given positions specified by colatitude and aximuthal angles. set_coefficients(coefficients) spherical_function(x, y, z) Returns the values of the spherical harmonics function at given - angular_function(theta, phi)¶
Returns the values of the spherical harmonics function at given positions specified by colatitude and aximuthal angles.
Parameters : theta : array-like, shape (K, )
The colatitude angles.
phi : array0-like, shape (K, )
The azimuth angles.
Returns : f : array-like, shape (K, )
The value of the function at given positions.
- set_coefficients(coefficients)¶
- spherical_function(x, y, z)¶
Returns the values of the spherical harmonics function at given positions specified by Cartesian coordinates.
Parameters : x, y, z : array-like, shape (K, )
Cartesian coordinates.
Returns : f : array-like, shape (K, )
The value of the function at given positions.
- phantomas.utils.shm.dimension(order)¶
Returns the dimension,
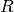, of the real, antipodally symmetric
spherical harmonics basis for a given truncation order.Parameters : order : int
The trunction order.
Returns : R : int
The dimension of the truncated spherical harmonics basis.
- phantomas.utils.shm.j(l, m)¶
Returns the flattened spherical harmonics index corresponding to degree l and order m.
Parameters : l : int
Degree of the spherical harmonics. Should be even.
m : int
Order of the spherical harmonics, should verify
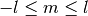
Returns : j : int
The associated index of the spherical harmonic.
- phantomas.utils.shm.l(j)¶
Returns the degree, l, of the spherical harmonic associated to index j.
Parameters : j : int
The flattened index of the spherical harmonic.
Returns : l : int
The associated even degree.
- phantomas.utils.shm.m(j)¶
Returns the order, m, of the spherical harmonic associated to index j.
Parameters : j : int
The flattened index of the spherical harmonic.
Returns : m : int
The associated order.
- phantomas.utils.shm.matrix(theta, phi, order=4)¶
Returns the spherical harmonics observation matrix.
Parameters : theta : array-like, shape (K, )
The colatitude angles.
phi : array-like, shape (K, )
The azimuth angles.
order : int
The spherical harmonics truncation order.
Returns : H : array-like, shape (K, R)
The spherical harmonics observation matrix.
tessellation Module¶
This module implements icosahedron tessellation to provide a (relatively) regular tessellation of the unit sphere.
- phantomas.utils.tessellation.compute_face_areas(vertices, faces)¶
Computes the (triangular) face areas.
Parameters : vertices : array-lie, (N, 3)
The array of vertices
faces : array-like
The array of triangles. Each triangle is a tuple with the indices of the 3 corresponding vertices.
- phantomas.utils.tessellation.compute_face_centers(vertices, faces)¶
Computes the (triangular) faces center of mass.
Parameters : vertices : array-lie, (N, 3)
The array of vertices
faces : array-like
The array of triangles. Each triangle is a tuple with the indices of the 3 corresponding vertices.
- phantomas.utils.tessellation.tessellation(order, face_centers=False, face_areas=False)¶
Constructs a tessellation from a subdivision of an icosahedron.
Parameters : order : int
The order of the recursive tessellation.
compute_face_centers : bool, optional
compute_face_areas : bool, optional
Returns : vertices : array-lie, (N, 3)
The array of vertices
faces : array-like
The array of triangles. Each triangle is a tuple with the indices of the 3 corresponding vertices.
nb_edges : int
Notes
We have only kept 10 faces out of 20, so as to generate a sphere tessellation adding the antipodal symmetric. Results are cached for future use in the dictionary _tessellations.
