mr_simul Package¶

`mr_simul` Package¶

This package contains implementation of the simulation of MR images and MR diffusion signal attenuation. The basic pipeline is as follows:

We first generate random images of T1, T2 relaxation times, for each tissue type (white matter, gray matter and cerebro-spinal fluid). See image_formation.relaxation_time_images().
From a description of the fiber bundles, we compute the local diffusion directions on a subdivision of the image grid. See fod.compute_directions().
Based on these diffusion directions, we compute a continuous FOD, using kernel density estimation. See fod.compute_fod().
Using a synthetic model of diffusion, we copmute the signal attenuation for the desired samples in Q-space, using convolution of the FOD by a fiber impulse response. See synthetic.AxiallySymmetricModel.signal() and synthetic.AxiallySymmetricModel.signal_convolution_sh().

`fod` Module¶

This module contains functions for the computation of the ground truth fiber orientation distribution (FOD) from a collection of fibers.

phantomas.mr_simul.fod.compute_directions(fibers, tangents, fiber_radii, voxel_center, voxel_size, resolution)¶

Given a set of fibers, and a voxel size, compute the set of orientations on a subgrid with associated weights.

Parameters :

fibers : sequence, length (M, )

A list of arrays.

tangents : sequence, length (M, )

A list of arrays.

fiber_radii : array-like, shape (M, )

The radius of each fiber bundle.

voxel_center : array-like shape (3, )

The center of the voxel where to compute the directions.

voxel_size : double

The voxel size in mm.

resolution : int

The resolution of the grid subdivision.

Returns :

fod_samples : array-like, shape (P, 3)

A sequence of diffusion directions, corresponding to local directions of fibers on the grid subdivision.

fod_weights : array-like, shape (P, )

A sequence of weights, corresponding to the volume fraction (relative to the voxel) of each diffusion direction.

phantomas.mr_simul.fod.compute_fod(fod_samples, fod_weights, dirs=None, kappa=30, sh=False, order_sh=8)¶

Computes fod from a discrete set of weighted samples, using kernel density estimation with a symmetric Von Mises-Fisher kernel.

Parameters :

fod_samples : array-like shape (P, 3)

A discrete set of directions, as obtained by compute_directions().

fod_weights : array-like shape (P, )

The volume fractions associated to the directions, as obtained by compute_directions().

dirs : array-like shape (M, 3)

The directions on which to evaluate the fod. If None, uses a default spherical 21-design (described in file spherical_21_design.txt).

kappa : double

The concentration factor of the Von Mises-Fischer distribution.

sh : bool

If True, returns the spherical harmonic coefficients of the fod.

order_sh : int

Truncation order of the spherical harmonic representation.

Returns :

fod : array-like, shape (M, )

The fod, evaluated at the specified directions.

`image_formation` Module¶

This module contains functions for MR image formation, such as random generation of T1/T2 relaxation time images, etc. In this regard, the mean and standard deviation of relaxation times of biological tissues, are taken from [R1].

References¶

[R1]	Wansapura, Janaka P., Scott K. Holland, R. Scott Dunn, and William S. Ball. “NMR relaxation times in the human brain at 3.0 tesla.” Journal of magnetic resonance imaging 9, no. 4 (1999): 531-538.

phantomas.mr_simul.image_formation.mr_signal(wm_vf, wm_t1, wm_t2, gm_vf, gm_t1, gm_t2, csf_vf, csf_t1, csf_t2, te, tr)¶

Computes MR image, provided images of the WM, GM, CSF and background volume fractions.

Parameters :

wm_vf : array-like, shape (dim_x, dim_y, dim_z)

White matter volume fraction.

wm_t1 : array-like, shape (dim_x, dim_y, dim_z)

White matter t1 relaxation image.

wm_t2 : array-like, shape (dim_x, dim_y, dim_z)

White matter t2 relaxation image.

gm_vf : array-like, shape (dim_x, dim_y, dim_z)

Gray matter volume fraction

gm_t1 : array-like, shape (dim_x, dim_y, dim_z)

Gray matter t1 relaxation image.

gm_t2 : array-like, shape (dim_x, dim_y, dim_z)

Gray matter t2 relaxation image.

csf_vf : array-like, shape (dim_x, dim_y, dim_z)

CSF volume fraction

csf_t1 : array-like, shape (dim_x, dim_y, dim_z)

CSF t1 relaxation image.

csf_t2 : array-like, shape (dim_x, dim_y, dim_z)

CSF t2 relaxation image.

background_vf : array-like, shape (dim_x, dim_y, dim_z)

Background volume fraction

te : double

echo time (s)

tr : double

repetition time (s)

Returns :

image : array-like, shape (dim_x, dim_y, dim_z)

The computed MR signal.

phantomas.mr_simul.image_formation.relaxation_time_images(image_shape, tissue_type)¶

Return randomly generated images of t1 and t2 relaxation times, of desired shape, for the desired tissue type.

Parameters :

image_shape : tuple

dim_x, dim_y, dim_z

tissue_type : ‘wm’, ‘gm’, ‘csf’

The tissue type, either white matter (WM), gray matter (GM), or cerebro-spinal fluid (CSF).

Returns :

t1 : array-like, shape (dim_x, dim_y, dim_z)

T1 relaxation time image.

t2 : array-like, shape (dim_x, dim_y, dim_z)

T2 relaxation time image.

phantomas.mr_simul.image_formation.rician_noise(image, sigma)¶

Add Rician distributed noise to the input image.

Parameters :

image : array-like, shape (dim_x, dim_y, dim_z) or ``(dim_x, dim_y,

dim_z, K)``

sigma : double

`partial_volume` Module¶

This module contains functions to compute partial volume effect, for fibers and other geometrical primitives.

phantomas.mr_simul.partial_volume.compute_affine_matrix(voxel_size, image_size)¶

Creates an affine matrix to compute real-world coordinates out of pixel coordinates. The convention is to return the coordinates of the center of the voxel.

Parameters :

voxel_size : double

The voxel size, in mm. NB: We assume isotropic voxel size.

image_size : double

The image size, in mm. NB: We assume the image has cubic dimensions.

Returns :

affine : array-lie, shape (4, 4)

The Nifti-like affine matrix.

phantomas.mr_simul.partial_volume.compute_corner_positions(voxel_size, image_size)¶

Computes the positions of voxel corners.

Parameters :

voxel_size : double

The voxel size, in mm.

image_size : array-like (3,)

The image size, in mm.

Returns :

corner_positions : array-like, shape (dim_x+1, dim_y+1, dim_z+1, 3)

phantomas.mr_simul.partial_volume.compute_fiber_masks(fibers, voxel_size, image_size)¶

Creates masks of the fibers. Voxels completely filled by the bundle are set to 2. Voxels which are intersected but not filled by the bundle are set to 1. Background is set to 0.

Parameters :

fibers : sequence, length (F, )

A sequence of Fiber instance (see phantomas.geometry.models.Fiber).

voxel_size : int

the voxel size in mm (voxels are isotropic).

image_size : int

the image size in mm (image is cubic).

phantomas.mr_simul.partial_volume.compute_spherical_region_masks(centers, radii, voxel_size, image_size)¶

Creates a mask of a list of spherical regions. Voxels completely filled by the region are set to 2. Voxels which are intersected by the region are set to 1. Background is set to 0.

Parameters :

centers : sequence of ndarray (3, )

Centers of the spherical regions.

radii : sequence

Radii of the spherical regions.

voxel_size : int

the voxel size in mm (voxels are isotropic).

image_size : int

the image size in mm (image is cubic).

phantomas.mr_simul.partial_volume.compute_volume_fractions(phantom_center, phantom_radius, gm_mask, fibers, fiber_masks, region_centers, region_radii, region_masks, voxel_size, image_size)¶

Computes the volume fraction of background and of each tissue type, for a given resolution.

Parameters :

phantom_center : array-like, shape (3, )

phantom_radius : double

gm_mask : array-like, shape (dim_x, dim_y, dim_z)

fibers : sequence of phantomas.geometry.models.Fiber

fiber_masks : array-like, shape (dim_x, dim_y, dim_z, nb_fibers)

region_centers : sequence of array-like

ragion_radii : sequence

region_masks : array-like, shape (dim_x, dim_y, dim_z, nb_regions)

voxel_size : double

image_size : double

Returns :

background_volume_fraction : array-like, shape (dim_x, dim_y, dim_z)

gm_volume_fraction : array-like, shape (dim_x, dim_y, dim_z)

wm_volume_fraction : array-like, shape (dim_x, dim_y, dim_z)

csf_volume_fraction : array-like, shape (dim_x, dim_y, dim_z)

phantomas.mr_simul.partial_volume.fibers_volume_fraction(fibers, intersect_codes, voxel_center, voxel_size, resolution=10)¶

Given a set of fibers and a voxel, returns the volume fraction of each fiber, the volume fraction of free water and the volume fraction of gray matter. The voxel is subdivided into a grid.

Parameters :

fibers : a sequence of Fiber instances

intersect_codes : a sequence of int (see Notes)

voxel_center : ndarray, shape (3,)

voxel_size : the voxel size in millimeter

resolution : int

the number of subdivision in each dimension.

Notes

intersect_codes[i] informs whether fiber i does not cross the voxel (0), simply intersects the voxel (1), or intersects the whole voxel (2).

phantomas.mr_simul.partial_volume.spherical_regions_volume_fraction(centers, radii, voxel_center, voxel_size, resolution=10)¶

Computes the volume fraction of a set of spherical regions.

Parameters :

centers : sequence of ndarray (3, ), centers of the spherical regions

radii : sequence of radius of the spherical regions

voxel_center : ndarray, shape (3,)

voxel_size : the voxel size in millimeter

resolution : int

the number of subdivision in each dimension.

`synthetic` Module¶

This module contains code to generate synthetic diffusion signal attenuation following several state-of-the-art model, including diffusion tensor [R2], stick model [R3], hindered diffusion in cylinder [R4], and mixture of the above. All the models described here have axial and antipodal symmetry, and we define an abstract class to serve as in interface.

References¶

[R2]	Peter J. Basser, James Mattiello, and Denis LeBihan. “MR diffusion tensor spectroscopy and imaging.” Biophysical journal 66, no. 1 (1994): 259-267

[R3]	T. E. J. Behrens, M. W. Woolrich, M. Jenkinson, H. Johansen-Berg, R. G. Nunes, S. Clare, P. M. Matthews, J. M. Brady, and S. M. Smith. “Characterization and propagation of uncertainty in diffusion-weighted MR Imaging.” Magnetic Resonance in Medicine 50, no. 5 (2003): 1077-1088.

[R4]	Soderman, Olle, and Bengt Jonsson. “Restricted diffusion in cylindrical geometry.” Journal of Magnetic Resonance, Series A 117, no. 1 (1995): 94-97.

class phantomas.mr_simul.synthetic.AxiallySymmetricModel¶

This class is an abstract class which defines the interface for all the synthetic models in use in phantomas.

Methods

`odf`(thetas[, tau])	Returns the ground truth ODF, when available.
`signal`(qnorms, thetas[, tau])	Returns the simulated signal attenuation.
`signal_convolution_sh`(order, qnorm[, tau, ...])	Returns the convolution operator in spherical harmonics basis, using

odf(thetas, tau=0.025330295910584444)¶

Returns the ground truth ODF, when available.

Parameters :

thetas : array-like, shape (K, )

Angles between the sampling directions and the axis.

tau : double

The diffusion time in s.

signal(qnorms, thetas, tau=0.025330295910584444)¶

Returns the simulated signal attenuation. The angles thetas correspond to the angles between the sampling directions and the principal axis of the diffusion model. Must be implemented in subclasses.

Parameters :

qnorms : array-like shape (K, )

The norm of q vectors in mm^-1.

thetas : array-like, shape (K, )

Angles between the sampling directions and the axis.

tau : double

Diffusion time in s.

signal_convolution_sh(order, qnorm, tau=0.025330295910584444, nb_samples=100)¶

Returns the convolution operator in spherical harmonics basis, using the Funk-Hecke theorem as described in [R5].

Parameters :

order : int

The (even) spherical harmonics truncation order.

qnorm : double

The norm of q vector in mm^-1.

tau : double

The diffusion time in s.

nb_samples : int

The number of samples controling the accuracy of the numerical integral.

References

[R5]	(1, 2) Descoteaux, Maxime. “High angular resolution diffusion MRI: from local estimation to segmentation and tractography.” PhD diss., Universite de Nice Sophia-Antipolis, France, 2010.

class phantomas.mr_simul.synthetic.GaussianModel(lambda1=0.0017, lambda2=0.0002)¶

Bases: phantomas.mr_simul.synthetic.AxiallySymmetricModel

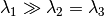This class models a Gaussian diffusion tensor wot axial symmetry. Typically, the eigenvalues of this tensors are $\lambda_1 \gg \lambda_2 = \lambda_3$ .

Parameters :

lambda1 : double

The eigenvalue associated with the principal direction, in mm²/s.

lambda2 : double

The eigenvalue associated with the two minor eigenvectors, in mm²/s.

Methods

`odf`(thetas[, tau])	Returns the ground truth ODF, when available.
`signal`(qnorms, thetas[, tau])	Returns the simulated signal attenuation, following the Stejskal
`signal_convolution_sh`(order, qnorm[, tau, ...])	Returns the convolution operator in spherical harmonics basis, using

signal(qnorms, thetas, tau=0.025330295910584444)¶

Returns the simulated signal attenuation, following the Stejskal and Tanner [1]_ equation. The angles thetas correspond to the angles between the sampling directions and the principal axis of the diffusion tensor.

Parameters :

qnorms : array-like shape (K, )

The norm of q vectors in mm^-1.

thetas : array-like, shape (K, )

Angles between the sampling directions and the axis.

tau : double

Diffusion time in the Stejskal and Tanner sequence in s.

mr_simul Package¶

`mr_simul` Package¶

`fod` Module¶

`image_formation` Module¶

References¶

`partial_volume` Module¶

`synthetic` Module¶

References¶

Table Of Contents

This Page

Navigation

mr_simul Package¶

mr_simul Package¶

fod Module¶

image_formation Module¶

References¶

partial_volume Module¶

synthetic Module¶

References¶

Table Of Contents

This Page

Quick search

Navigation

`mr_simul` Package¶

`fod` Module¶

`image_formation` Module¶

`partial_volume` Module¶

`synthetic` Module¶